Dashboard Masticationpedia/Wellcome project

Interpretazione della figura: spazio di Hilbert e valore medio osservabile

La figura illustra uno dei principi cardine del modello *quantum-like* sviluppato nel progetto Wellcome – Masticationpedia Paradigm Initiative: il comportamento neuromuscolare non viene interpretato come una sequenza deterministica di eventi, ma come una **distribuzione di stati funzionali** all’interno di uno spazio di Hilbert multidimensionale.

In questo quadro teorico, ogni vettore rappresenta una possibile configurazione di reclutamento motorio, mentre la freccia blu ⟨A⟩ indica la **media statistica degli osservabili** ottenuta a partire dall’operatore densità $\rho$. La figura rende visibile un concetto chiave: > il segnale EMG che osserviamo clinicamente non è la fotografia di un evento unico, ma la sovrapposizione probabilistica di molteplici micro-stati.

Questa rappresentazione non mira a diagnosticare una lesione specifica, bensì a mostrare come la **coerenza funzionale** e la **simmetria bilaterale** emergano come proprietà statistiche globali del sistema, esattamente come in un modello di stato misto quantistico.

---

1° Step: Rappresentazione quantistica mista dello schema di reclutamento motorio nell’EMG

Il segnale elettromiografico (EMG) di superficie dei muscoli masseteri può essere interpretato come la **proiezione (o misura)** di uno **stato misto** definito su uno spazio di Hilbert finito, i cui vettori di base rappresentano le diverse configurazioni di reclutamento delle unità motorie.

Il tracciato d’interferenza visibile nell’EMG può essere così descritto come il risultato della **sovrapposizione vettoriale** e delle **relazioni di fase** tra questi stati elementari, in modo analogo alle strutture d’interferenza osservate in un sistema quantistico.

1. Spazio degli stati e vettori base

Sia ${\mathscr{H}}$ uno spazio di Hilbert complesso generato da un insieme di vettori di base che rappresentano i modelli di reclutamento motorio:

${\mathscr{H}}=\mathrm{s}\mathrm{p}\mathrm{a}\mathrm{n}\{|e_1⟩,|e_2⟩,\dots ,|e_d⟩\}$

Ogni vettore \(|e_k\rangle\) corrisponde a un pattern fisiologicamente significativo (unità motorie a bassa soglia, ad alta soglia, co-attivazioni sinergiche, ecc.).

2. Stati puri e stati misti

Uno **stato puro** è un vettore unitario \(|\psi\rangle \in \mathcal{H}\), descritto dall’operatore di densità:

$\rho =|\psi ⟩⟨\psi |$

Uno **stato misto** è invece una combinazione convessa di stati puri:

$$\begin{gathered} \rho =\sum _{j=1}^m{p}_j|{\psi }_j⟩⟨{\psi }_j|,p_j\ge 0, \\ \sum _j{p}_j=1 \end{gathered}$$

Dal punto di vista fisiologico, \(\rho\) rappresenta la **variabilità stocastica** e la **micro-eterogeneità** del reclutamento motorio nel tempo (fatica, input riflessi, rumore di fondo).

3. Osservabili: dominio del tempo e delle frequenze

Il segnale EMG misurato nel tempo \(t\) può essere espresso come valore atteso di un operatore osservabile \(A(t)\):

$x(t)=\mathrm{Tr}[\rho A(t)]$

Analogamente, la potenza spettrale in una banda di frequenza \(B\) si scrive:

$P(B)=\mathrm{Tr}[\rho S(B)]$

dove \(S(B)\) rappresenta un operatore positivo che aggrega il contributo dei modi di reclutamento nella banda \(B\).

4. Struttura di interferenza

Scrivendo uno stato puro come \(|\psi\rangle = \sum_k c_k |e_k\rangle\), si ha:

$x_{\psi }(t)=⟨\psi |A(t)|\psi ⟩=\sum _{k,\ell }{c}_k\overline{c_{\ell }}⟨e_{\ell }|A(t)|e_k⟩$

I termini diagonali (\(k=\ell\)) rappresentano la **potenza dei modi**, mentre quelli fuori diagonale (\(k\neq \ell\)) descrivono le **coerenze di fase** o “interferenze”. Per uno stato misto, tali contributi sono pesati dalle probabilità \(p_j\) dei singoli stati \(|\psi_j\rangle\).

5. Modellazione bilaterale (masseteri sinistro e destro)

Per rappresentare la sinergia bilaterale si usa un sistema bipartito:

${\mathscr{H}}={{\mathscr{H}}}_L\otimes {{\mathscr{H}}}_R,\rho \in {𝒮}({{\mathscr{H}}}_L\otimes {{\mathscr{H}}}_R)$

I segnali \(x_L(t)\) e \(x_R(t)\) corrispondono rispettivamente alle aspettative di \(A_L(t)\otimes I\) e \(I\otimes A_R(t)\). La correlazione sincrona tra i due lati (co-contrazione) è modellata da:

$\mathrm{\Gamma }(t)=\mathrm{Tr}[\rho (A_L(t)\otimes A_R(t))]$

Il termine “quantistico” va inteso **in senso analogico e matematico**, non come fenomeno fisico di entanglement.

6. Collegamento con la trasformata di Fourier

Definendo la trasformata di Fourier del segnale temporale:

$X(f)=\int x(t)e^{-i2\pi ft}dt$

si ottiene:

$X(f)=\mathrm{Tr}[\rho \tilde{A}(f)]$

con \(\widetilde{A}(f)\) operatore di frequenza. La potenza di banda risulta:

$P(B)=\underset{B}{\int }|X(f){|}^{2}df=\mathrm{Tr}[\rho S(B)]$

7. Esempio di stato misto a tre modi

Sia \(|e_1\rangle, |e_2\rangle, |e_3\rangle\) la base di tre modalità di reclutamento (lento, intermedio, rapido). Uno stato misto semplice è:

$\rho =p_1|{\psi }_1⟩⟨{\psi }_1|+p_2|{\psi }_2⟩⟨{\psi }_2|,|{\psi }_1⟩=\alpha |e_1⟩+\beta |e_2⟩,|{\psi }_2⟩=\gamma |e_2⟩+\delta |e_3⟩$

con \(p_1+p_2=1\). Le componenti fuori diagonale \(\langle e_\ell|A(t)|e_k\rangle\) producono l’effetto d’interferenza osservabile nel tracciato EMG e nei picchi dello spettro \(X(f)\).

8. Significato clinico-analitico

• **Occupanze** (\(\pi_k = \operatorname{Tr}[\rho |e_k\rangle\langle e_k|]\)): rappresentano la prevalenza relativa dei diversi schemi di reclutamento (es. fatica o iperattività).
• **Coerenze** (\(\rho_{k\ell},\ k\neq \ell\)): esprimono la stabilità o la sincronia dei pattern coordinati (es. tremori, oscillazioni ritmiche).
• **Asimmetrie** (\(\rho_L\) vs \(\rho_R\)): differenze tra i due lati dei masseteri, utili a identificare squilibri funzionali.
• **Marcatori spettrali**: i picchi nel dominio di frequenza rappresentano la manifestazione macroscopica delle coerenze vettoriali nello spazio di stato.

9. Limitazioni del modello

Il modello “quantum-like” è **puramente matematico** e non implica fenomeni quantistici fisici nei tessuti biologici. L’analisi EMG fornisce informazioni periferiche sul reclutamento muscolare e **non** permette diagnosi dirette di patologie cerebrali.

10. Sintesi per il progetto Wellcome – Masticationpedia Paradigm Initiative

L’approccio propone di rappresentare i pattern di reclutamento motorio come vettori in uno spazio di Hilbert finito. Il segnale EMG è descritto come la media (traccia) di osservabili temporali e spettrali rispetto a uno stato misto \(\rho\):

$x(t)=\mathrm{T}\mathrm{r}[\rho A(t)],X(f)=\mathrm{T}\mathrm{r}[\rho \tilde{A}(f)]$

Le componenti diagonali di \(\rho\) rappresentano la distribuzione dei modi di reclutamento, mentre quelle fuori diagonale descrivono la coerenza dinamica. La modellazione bilaterale consente di studiare la coordinazione sinistra-destra dei masseteri attraverso osservabili di correlazione, aprendo nuove prospettive diagnostiche nel dolore orofacciale e nella neurognatologia evocata.

---

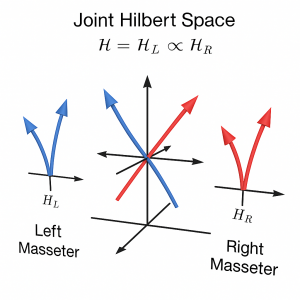
Interpretazione dello spazio di Hilbert congiunto dei masseteri

La figura tridimensionale rappresenta in forma schematica il **Joint Hilbert Space** dei due muscoli masseteri, modellato come:

${\mathscr{H}}={{\mathscr{H}}}_L\otimes {{\mathscr{H}}}_R$

dove:

• ${{\mathscr{H}}}_L$ è lo spazio di Hilbert associato ai **modi di reclutamento del massetere sinistro**;
• ${{\mathscr{H}}}_R$ è lo spazio di Hilbert del **massetere destro**.

Ogni freccia nel diagramma corrisponde a un vettore di stato o a una proiezione (operatore osservabile) che agisce in uno di questi sottospazi.

---

🔵 Significato delle frecce blu (massetere sinistro)

1. La freccia bidimensionale “a V” (sulla sinistra)

Rappresenta lo spazio locale degli stati del massetere sinistro, ossia l’insieme delle possibili configurazioni di reclutamento delle unità motorie:

$|e_1⟩,|e_2⟩\in {{\mathscr{H}}}_L$

La forma “a V” indica che questo sottosistema contiene più di un modo attivo, ognuno con la propria ampiezza di probabilità. Il grado di apertura della “V” diventa così una **metafora visiva dell’operatore densità**, che descrive la distribuzione probabilistica del reclutamento motorio.

Formalmente, l’operatore densità è:

${\rho }_L=\sum _i{p}_i|e_i⟩⟨e_i|$

L’apertura della “V” rappresenta quindi la **varianza probabilistica** (o eterogeneità) dei modi di attivazione.

→ In sintesi: la “V” blu corrisponde all’**operatore densità** ${\rho }_L$, e la sua ampiezza simboleggia la dispersione statistica del reclutamento muscolare.

---

2. Le frecce blu tridimensionali nel piano centrale

Rappresentano la **proiezione della densità locale** ${\rho }_L$ nello spazio congiunto:

${\rho }_{LR}={\rho }_L\otimes {\rho }_R$

oppure, in presenza di correlazioni sinergiche, in uno **stato non separabile**:

$\rho \ne {\rho }_L\otimes {\rho }_R$

Graficamente, le frecce blu che si dirigono verso il centro del cubo rappresentano la porzione di attività sinistra che **partecipa alla coordinazione bilaterale**, ossia la parte di varianza EMG sincronizzata con il lato destro.

---

🔴 Significato delle frecce rosse (massetere destro)

Le frecce rosse hanno lo stesso significato ma riferito al sottospazio ${{\mathscr{H}}}_R$ e alla densità ${\rho }_R$. L’intersezione tra frecce blu e rosse nel centro del diagramma indica la **regione di attività congiunta**, rappresentata matematicamente dall’operatore di correlazione:

$C(t)=A_L(t)\otimes A_R(t)$

e dal suo valore atteso:

$\mathrm{\Gamma }(t)=\mathrm{Tr}[\rho C(t)]$

Questo termine descrive la **sincronia bilaterale** o la **co-contrazione funzionale** tra i due masseteri.

---

🧩 Tabella riassuntiva

Elemento grafico	Significato matematico	Interpretazione fisiologica
Freccia blu “a V”	${\rho }_L$ – operatore densità (varianza)	Dispersione probabilistica del reclutamento sinistro
Freccia rossa “a V”	${\rho }_R$ – operatore densità (varianza)	Dispersione probabilistica del reclutamento destro
Frecce 3D blu/rosse che convergono	${{\mathscr{H}}}_L\otimes {{\mathscr{H}}}_R$	Coordinazione bilaterale dei pattern motori
Zona di sovrapposizione centrale	$\rho$ non separabile	Coerenza funzionale o sinergia neuro-muscolare

---

💡 Interpretazione clinica

• La **sincronia fisiologica** tra i due lati riflette una coordinazione masticatoria o posturale corretta.
• Le **asimmetrie** o la **decorrelazione** dei segnali indicano possibili disfunzioni neuromuscolari o compensazioni patologiche.
• Il modello matematico consente di quantificare la **coerenza funzionale** e la **probabilità di reclutamento simultaneo** in modo rigoroso.

---

📘 Nota esplicativa per la pubblicazione Masticationpedia

Il diagramma 3D mostra come i sottospazi di Hilbert ${{\mathscr{H}}}_L$ e ${{\mathscr{H}}}_R$ vengano combinati in un unico spazio composito. Le frecce colorate indicano le componenti di stato dei due muscoli, mentre la loro intersezione centrale rappresenta la regione di correlazione funzionale descritta da:

$\mathrm{\Gamma }(t)=\mathrm{Tr}[\rho (A_L(t)\otimes A_R(t))]$

Questa rappresentazione fornisce una chiave visiva per comprendere la **logica vettoriale** del reclutamento bilaterale dei masseteri all’interno del modello *quantum-like* della neurognatologia evocata. ---

---

⚖️ Limiti epistemologici dello stato misto quantistico

Nel modello *quantum-like* applicato all’EMG, lo stato del sistema neuromuscolare viene descritto tramite un **operatore densità** $\rho$ che rappresenta una miscela statistica di più configurazioni di reclutamento:

$\rho =\sum _i{p}_i|{\psi }_i⟩⟨{\psi }_i|$

Il valore medio di un osservabile (ad esempio la potenza spettrale o la coerenza bilaterale) si ottiene come:

$⟨A⟩=\mathrm{Tr}[\rho A]$

Tale media fornisce una misura del comportamento complessivo del sistema, ma non è in grado di evidenziare **segni specifici di lesione organica o di asimmetria patologica**. Infatti, la natura probabilistica dello stato misto implica che le componenti anomale o asimmetriche possano risultare “compensate” all’interno della somma delle probabilità.

---

🧠 Significato concettuale

Lo spazio di Hilbert rappresenta **tutte le possibilità di stato** del sistema neuromuscolare. Quando il sistema si trova in uno stato misto, ciò che viene osservato sperimentalmente (ad esempio l’interferenza EMG) è il risultato di una **media statistica** su molteplici micro-stati funzionali, ciascuno dei quali può essere fisiologico o alterato.

Questa media statistica non consente una **diagnosi diretta** di una lesione neurologica o organica, poiché le informazioni specifiche sullo stato patologico restano “nascoste” nella struttura interna dell’operatore densità.

---

📊 Rappresentazione grafica nel diagramma 3D

Nel diagramma tridimensionale dello spazio di Hilbert congiunto:

• Le frecce blu e rosse rappresentano le componenti di stato dei due masseteri (${{\mathscr{H}}}_L$ e ${{\mathscr{H}}}_R$);
• L’area centrale di sovrapposizione illustra la **coerenza bilaterale media** ($\mathrm{\Gamma }(t)$);
• L’insieme delle frecce nel volume cubico visualizza la **somma e la media degli operatori densità**, i cui vettori risultanti non mostrano un segno marcato di asimmetria.

---

💬 Interpretazione clinica

L’assenza di un vettore risultante fortemente direzionato o deformato nello spazio di Hilbert indica che il sistema si trova in una **condizione di equilibrio statistico** — coerente con un’attività neuromuscolare complessivamente simmetrica. Tuttavia, tale equilibrio non esclude la presenza di **micro-alterazioni neurologiche** o **danni organici**: semplicemente, esse non emergono nel valore medio misurato, perché la descrizione quantistica mista è **non-deterministica**.

---

🧭 Nota concettuale per la ricerca

Il modello *quantum-like* non mira a sostituire la diagnostica clinica diretta, ma a fornire un **quadro matematico di probabilità funzionale**, nel quale la fisiologia viene interpretata come un insieme di stati sovrapposti. La mancata “diagnosticità” dello stato misto non rappresenta un limite, bensì una **proprietà epistemologica intrinseca**: il modello descrive il *come* un sistema funziona, non *che cosa* lo danneggia.

In tal senso, il paradigma *quantum-like* di Masticationpedia costituisce una base teorica per lo sviluppo di **metriche di coerenza funzionale** che potranno, in futuro, integrarsi con i metodi diagnostici neuro-fisiologici classici.

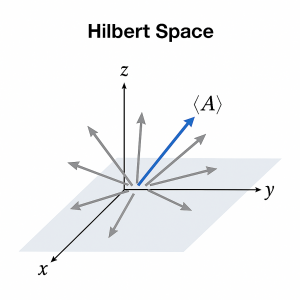
== Interpretazione della figura: spazio di Hilbert e valore medio osservabile ==

La figura rappresenta lo **spazio di Hilbert** nel quale si collocano tutti i possibili stati funzionali neuromuscolari del sistema masticatorio. Ogni vettore nello spazio tridimensionale corrisponde a una specifica configurazione di reclutamento delle unità motorie, come nel modello EMG.

---

🎯 Struttura generale della figura

• Il **piano grigio** rappresenta lo spazio tridimensionale di Hilbert, le cui dimensioni (x, y, z) corrispondono a diversi parametri funzionali: forza, frequenza, sincronizzazione.
• Le **frecce grigie** che partono dall’origine sono i **vettori di stato** $|{\psi }_i⟩$, ognuno dei quali rappresenta una possibile configurazione istantanea del sistema muscolare.

---

🔶 Origine dello spazio

Il punto d’origine, dove si incontrano gli assi x, y e z, indica il **centro di equilibrio statistico** del sistema, ossia la condizione neutra in cui nessun lato (destro o sinistro) prevale. Tutte le frecce partono da questo punto, poiché ogni stato funzionale viene descritto come deviazione rispetto all’equilibrio.

---

🔷 La freccia blu (⟨A⟩)

La **freccia blu**, indicata come $⟨A⟩$, rappresenta la **media vettoriale** di tutte le frecce grigie, cioè il **valore medio di un osservabile** del sistema.

In termini matematici:

$⟨A⟩=\mathrm{Tr}[\rho A]$

dove:

• $A$ = operatore osservabile (una grandezza misurabile, ad esempio la potenza EMG o la coerenza bilaterale);
• $\rho$ = operatore densità, che descrive la probabilità di ciascun stato;
• $⟨A⟩$ = media ponderata di tutti i contributi di stato.

La freccia blu rappresenta quindi la **sintesi probabilistica** del comportamento complessivo del sistema neuromuscolare.

---

🧠 Significato concettuale

Le frecce grigie corrispondono ai **micro-stati locali** di attività del muscolo massetere: ciascuna indica un diverso schema di reclutamento delle unità motorie. Il muscolo non opera mai in uno stato singolo, ma in una **sovrapposizione dinamica** di molte configurazioni.

La freccia blu $⟨A⟩$ indica la **media** di tutti questi stati e corrisponde al segnale EMG osservabile nel dominio macroscopico.

---

⚖️ Conseguenza diagnostica

Se le frecce grigie sono distribuite **in modo simmetrico** e la freccia blu $⟨A⟩$ è **centrata e di piccola ampiezza**, il sistema si trova in una condizione di:

• equilibrio funzionale complessivo,
• assenza di direzione dominante,
• e quindi **assenza di segni evidenti di asimmetria o danno neurologico**.

Tuttavia, ciò non implica che non esistano alterazioni locali: il modello a stato misto descrive solo **medie statistiche**, non eventi deterministici.

---

📘 Riassunto sintetico

Elemento grafico	Simbolo	Significato
Frecce grigie	$|{\psi }_i⟩$	Micro-stati o configurazioni locali del sistema
Piano grigio	${\mathscr{H}}$	Spazio di Hilbert delle possibilità funzionali
Punto d’origine	—	Stato di equilibrio statistico
Freccia blu	$⟨A⟩=\mathrm{Tr}[\rho A]$	Media osservabile del sistema (valore atteso)
Distribuzione simmetrica dei vettori	—	Assenza di asimmetria patologica o lesione evidente

---

💬 Interpretazione clinica

La distribuzione simmetrica dei vettori nello spazio di Hilbert e la ridotta ampiezza del vettore medio $⟨A⟩$ indicano una condizione di **equilibrio funzionale bilaterale**. Ciò suggerisce che, pur esistendo fluttuazioni locali o micro-alterazioni, il sistema mantiene una **coerenza globale** compatibile con la normalità fisiologica.

---

📍 Nota concettuale finale

Il modello a stato misto quantistico non è uno strumento diagnostico diretto, ma un **modello descrittivo** del comportamento probabilistico del sistema neuromuscolare. Esso fornisce una mappa delle *possibilità funzionali*, non un referto clinico di danno organico. Il suo valore risiede nella capacità di rappresentare matematicamente la **complessità coordinativa** e la **coerenza statistica** della funzione masticatoria.

⚙️ Normalizzazione dello stato misto

Nel modello *quantum-like* di Masticationpedia, lo stato funzionale del sistema neuromuscolare viene espresso tramite l’operatore densità:

$\rho =\sum _i{p}_i|{\psi }_i⟩⟨{\psi }_i|$

dove i coefficienti $p_i$ rappresentano le probabilità relative delle diverse configurazioni di reclutamento motorio. Affinché lo stato abbia significato fisico e comparativo, deve essere **normalizzato** secondo la condizione:

$\mathrm{Tr}[\rho ]=\sum _i{p}_i=1$

La normalizzazione garantisce che l’intero spazio di Hilbert rappresenti un sistema unitario e coerente, in cui tutte le possibilità funzionali sommano a un unico “peso probabilistico” globale.

---

💬 Interpretazione fisiologica

In termini biologici, la normalizzazione di $\rho$ equivale a considerare il sistema neuromuscolare come un’entità omeostatica: anche se le singole unità motorie variano la propria attivazione, il sistema mantiene una distribuzione complessiva costante nel tempo. Questo implica che:

• il segnale EMG osservato è sempre riferito a una base probabilistica normalizzata,
• le variazioni patologiche o asimmetriche emergono solo come **deformazioni interne** alla distribuzione, non come variazioni del totale.

---

📊 Valore diagnostico della normalizzazione

La condizione di normalizzazione consente di: 1. confrontare soggetti diversi o sessioni differenti sullo stesso piano funzionale; 2. distinguere variazioni fisiologiche (omeostatiche) da alterazioni effettive della coerenza; 3. formulare indici quantitativi di asimmetria probabilistica come deviazioni dalla traccia unitaria.

In sintesi, la normalizzazione dello stato misto fornisce la base matematica per interpretare la simmetria funzionale del sistema masticatorio come una proprietà di equilibrio statistico e non come un dato grezzo di ampiezza del segnale.

---

---

Interpretazione della figura: spazio di Hilbert e valore medio osservabile

La figura illustra uno dei principi cardine del modello *quantum-like* sviluppato nel progetto Wellcome – Masticationpedia Paradigm Initiative: il comportamento neuromuscolare non viene interpretato come una sequenza deterministica di eventi, ma come una **distribuzione di stati funzionali** all’interno di uno spazio di Hilbert multidimensionale.

In questo quadro teorico, ogni vettore rappresenta una possibile configurazione di reclutamento motorio, mentre la freccia blu $⟨A⟩$ indica la **media statistica degli osservabili** ottenuta a partire dall’operatore densità $\rho$. La figura rende visibile un concetto chiave: > il segnale EMG che osserviamo clinicamente non è la fotografia di un evento unico, ma la sovrapposizione probabilistica di molteplici micro-stati.

Questa rappresentazione non mira a diagnosticare una lesione specifica, bensì a mostrare come la **coerenza funzionale** e la **simmetria bilaterale** emergano come proprietà statistiche globali del sistema, esattamente come in un modello di stato misto quantistico.

---

1° Step: Rappresentazione quantistica mista dello schema di reclutamento motorio nell’EMG

Il segnale elettromiografico (EMG) di superficie dei muscoli masseteri può essere interpretato come la **proiezione (o misura)** di uno **stato misto** definito su uno spazio di Hilbert finito, i cui vettori di base rappresentano le diverse configurazioni di reclutamento delle unità motorie.

Il tracciato d’interferenza visibile nell’EMG può essere così descritto come il risultato della **sovrapposizione vettoriale** e delle **relazioni di fase** tra questi stati elementari, in modo analogo alle strutture d’interferenza osservate in un sistema quantistico.

1. Spazio degli stati e vettori base

Sia ${\mathscr{H}}$ uno spazio di Hilbert complesso generato da un insieme di vettori di base che rappresentano i modelli di reclutamento motorio:

${\mathscr{H}}=\mathrm{s}\mathrm{p}\mathrm{a}\mathrm{n}\{|e_1⟩,|e_2⟩,\dots ,|e_d⟩\}$

Ogni vettore $|e_k⟩$ corrisponde a un pattern fisiologicamente significativo (unità motorie a bassa soglia, ad alta soglia, co-attivazioni sinergiche, ecc.).

2. Stati puri e stati misti

Uno **stato puro** è un vettore unitario $|\psi ⟩\in {\mathscr{H}}$, descritto dall’operatore di densità:

$\rho =|\psi ⟩⟨\psi |$

Uno **stato misto** è invece una combinazione convessa di stati puri:

$$\begin{gathered} \rho =\sum _{j=1}^m{p}_j|{\psi }_j⟩⟨{\psi }_j|,p_j\ge 0, \\ \sum _j{p}_j=1 \end{gathered}$$

Dal punto di vista fisiologico, $\rho$ rappresenta la **variabilità stocastica** e la **micro-eterogeneità** del reclutamento motorio nel tempo (fatica, input riflessi, rumore di fondo).

3. Osservabili: dominio del tempo e delle frequenze

Il segnale EMG misurato nel tempo $t$ può essere espresso come valore atteso di un operatore osservabile $A(t)$:

$x(t)=\mathrm{Tr}[\rho A(t)]$

Analogamente, la potenza spettrale in una banda di frequenza $B$ si scrive:

$P(B)=\mathrm{Tr}[\rho S(B)]$

dove $S(B)$ rappresenta un operatore positivo che aggrega il contributo dei modi di reclutamento nella banda $B$.

4. Struttura di interferenza

Scrivendo uno stato puro come $|\psi ⟩=\sum _k{c}_k|e_k⟩$, si ha:

$x_{\psi }(t)=⟨\psi |A(t)|\psi ⟩=\sum _{k,\ell }{c}_k\overline{c_{\ell }}⟨e_{\ell }|A(t)|e_k⟩$

I termini diagonali ($k=\ell$) rappresentano la **potenza dei modi**, mentre quelli fuori diagonale ($k\ne \ell$) descrivono le **coerenze di fase** o “interferenze”. Per uno stato misto, tali contributi sono pesati dalle probabilità $p_j$ dei singoli stati $|{\psi }_j⟩$.

5. Modellazione bilaterale (masseteri sinistro e destro)

Per rappresentare la sinergia bilaterale si usa un sistema bipartito:

${\mathscr{H}}={{\mathscr{H}}}_L\otimes {{\mathscr{H}}}_R,\rho \in {𝒮}({{\mathscr{H}}}_L\otimes {{\mathscr{H}}}_R)$

I segnali $x_L(t)$ e $x_R(t)$ corrispondono rispettivamente alle aspettative di $A_L(t)\otimes I$ e $I\otimes A_R(t)$. La correlazione sincrona tra i due lati (co-contrazione) è modellata da:

$\mathrm{\Gamma }(t)=\mathrm{Tr}[\rho (A_L(t)\otimes A_R(t))]$

Il termine “quantistico” va inteso **in senso analogico e matematico**, non come fenomeno fisico di entanglement.

6. Collegamento con la trasformata di Fourier

Definendo la trasformata di Fourier del segnale temporale:

$X(f)=\int x(t)e^{-i2\pi ft}dt$

si ottiene:

$X(f)=\mathrm{Tr}[\rho \tilde{A}(f)]$

con $\tilde{A}(f)$ operatore di frequenza. La potenza di banda risulta:

$P(B)=\underset{B}{\int }|X(f){|}^{2}df=\mathrm{Tr}[\rho S(B)]$

7. Esempio di stato misto a tre modi

Sia $|e_1⟩,|e_2⟩,|e_3⟩$ la base di tre modalità di reclutamento (lento, intermedio, rapido). Uno stato misto semplice è:

$\rho =p_1|{\psi }_1⟩⟨{\psi }_1|+p_2|{\psi }_2⟩⟨{\psi }_2|,|{\psi }_1⟩=\alpha |e_1⟩+\beta |e_2⟩,|{\psi }_2⟩=\gamma |e_2⟩+\delta |e_3⟩$

con $p_1+p_2=1$. Le componenti fuori diagonale $⟨e_{\ell }|A(t)|e_k⟩$ producono l’effetto d’interferenza osservabile nel tracciato EMG e nei picchi dello spettro $X(f)$.

8. Significato clinico-analitico

• **Occupanze** (${\pi }_k=\mathrm{Tr}[\rho |e_k⟩⟨e_k|]$): rappresentano la prevalenza relativa dei diversi schemi di reclutamento (es. fatica o iperattività).
• **Coerenze** ($$\begin{gathered} {\rho }_{k\ell }, \\ k\ne \ell \end{gathered}$$): esprimono la stabilità o la sincronia dei pattern coordinati (es. tremori, oscillazioni ritmiche).
• **Asimmetrie** (${\rho }_L$ vs ${\rho }_R$): differenze tra i due lati dei masseteri, utili a identificare squilibri funzionali.
• **Marcatori spettrali**: i picchi nel dominio di frequenza rappresentano la manifestazione macroscopica delle coerenze vettoriali nello spazio di stato.

9. Limitazioni del modello

Il modello “quantum-like” è **puramente matematico** e non implica fenomeni quantistici fisici nei tessuti biologici. L’analisi EMG fornisce informazioni periferiche sul reclutamento muscolare e **non** permette diagnosi dirette di patologie cerebrali.

10. Sintesi per il progetto Wellcome – Masticationpedia Paradigm Initiative

L’approccio propone di rappresentare i pattern di reclutamento motorio come vettori in uno spazio di Hilbert finito. Il segnale EMG è descritto come la media (traccia) di osservabili temporali e spettrali rispetto a uno stato misto $\rho$:

$x(t)=\mathrm{T}\mathrm{r}[\rho A(t)],X(f)=\mathrm{T}\mathrm{r}[\rho \tilde{A}(f)]$

Le componenti diagonali di $\rho$ rappresentano la distribuzione dei modi di reclutamento, mentre quelle fuori diagonale descrivono la coerenza dinamica. La modellazione bilaterale consente di studiare la coordinazione sinistra-destra dei masseteri attraverso osservabili di correlazione, aprendo nuove prospettive diagnostiche nel dolore orofacciale e nella neurognatologia evocata.